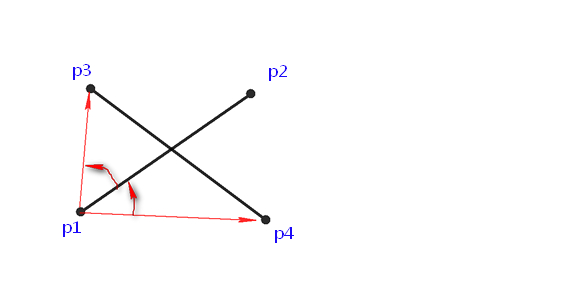
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
package geometry;
import java.util.Scanner;
public class Segment {
private int direction(int[] pi, int[] pj, int[] pk){
return (pi[0]-pk[0])*(pi[1]-pj[1]) - (pi[0]-pj[0])*(pi[1]-pk[1]);
}
private boolean onSegment(int[] pi, int[] pj, int[] pk) {
if ( Math.min(pi[0], pj[0]) <= pk[0] && pk[0] <= Math.max(pi[0], pj[0]) &&
Math.min(pi[1], pj[1]) <= pk[1] && pk[1] <= Math.max(pi[1], pj[1]) ) {
return true;
}else {
return false;
}
}
public boolean segmentInsert(int[] p1, int[] p2, int[] p3, int[] p4) {
int d1 = direction(p3, p4, p1);
int d2 = direction(p3, p4, p2);
int d3 = direction(p1, p2, p3);
int d4 = direction(p1, p2, p4);
if ( ((d1>0 && d2<0) || (d1<0 && d2>0)) &&
((d3>0 && d4<0) || (d3<0 && d4>0))) {
return true;
} else if ( d1==0 && onSegment(p3, p4, p1)) {
return true;
} else if ( d2==0 && onSegment(p3, p4, p2)) {
return true;
} else if ( d3==0 && onSegment(p1, p2, p3)) {
return true;
} else if ( d4==0 && onSegment(p1, p2, p4)) {
return true;
} else {
return false;
}
}
public static void main(String[] args){
Segment segment = new Segment();
Scanner in = new Scanner(System.in);
int[] p1 = {in.nextInt(), in.nextInt()};
int[] p2 = {in.nextInt(), in.nextInt()};
int[] p3 = {in.nextInt(), in.nextInt()};
int[] p4 = {in.nextInt(), in.nextInt()};
if (segment.segmentInsert(p1, p2, p3, p4)) {
System.out.println("相交");
} else {
System.out.println("不相交");
}
}
}
|