并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。
我们先看一个简单的例子:
例子:越多越好
问题描述
某公司要求它的一些员工从事若干个项目。因这些项目相当复杂,项目是分期进行的,但每个项目需要熟悉该项目的人数越多越好。当然对人员有一定的要求。
公司的员工很多,达10000人,编号从1到10000。员工们中如果有人熟悉这个项目,那么与其认识的人只要讨教一些技巧后也能知道项目如何进行,经过传帮带后所有与其直接或间接认识的人也掌握了从事项目的技巧。为便于交流与项目修改,要求从事项目的人都直接或间接认识。
现在给定直接认识的人员对,您应该做出正确的选择。
输入
有若干个项目。每个项目的数据中第一行是一个整数n (0 ≤ n ≤ 100000) ,即该项目中直接认识的人数对。接下来有n行,每行是一个用空格隔开的数对A和B,表示他们认识,(A ≠ B, 1 ≤ A, B ≤ 10000000) 。
输出
对每个项目输出从事项目的最大人数。
输入样例
4
1 2
3 4
5 6
1 6
4
1 2
3 4
5 6
7 8
输出样例
4
2
首先进行初始化,将每个元素看作一个树,他们的父节点指向自己。
然后将想认识的两个人看作一个集合,修改元素的根节点:{1,2},{3,4},{5,6},{1,6}。
将每个集合构造一个树:
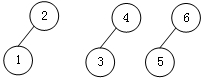
当执行到{1,6} 是,查询 1 的根节点是 2,这时就将 6 根节点(即自己)和 1 的根节点连接,从中选择一个做根节点。
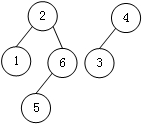
这是就可以看出最多的一组就是 2 为根节点的那一组,即输出 4。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
|
package union.find;
import java.util.Scanner;
public class Exec1 {
int[] father;
int[] son;
final int num = 1000;
private void init(){
father = new int[num+1];
son = new int[num+1];
for (int i = 0; i < father.length; i++) {
father[i] = i;
son[i] = 0;
}
}
private int findRoot(int s) {
if (s != father[s]) {
father[s] = findRoot(father[s]);
}
return father[s];
}
private void union(int x, int y) {
x = findRoot(x);
y = findRoot(y);
if (x == y) {
return;
}
if (son[x] > son[y]) {
father[y] = x;
son[x] = son[x] + son[y] + 1;
} else {
father[x] = y;
son[y] = son[y] + son[x] +1;
}
}
public void start(){
Scanner in = new Scanner(System.in);
int n = in.nextInt();
init();
for (int i = 1; i < n+1; i++) {
int x = in.nextInt();
int y = in.nextInt();
union(x, y);
}
}
public int max() {
int max = 1;
for(int i=2;i<=num;i++)
if( son[max] < son[i])
max = i;
return son[max]+1;
}
public static void main(String[] args) {
Exec1 exec1 = new Exec1();
exec1.start();
System.out.println(exec1.max());
}
}
|
并查集的精髓(即三个操作)
- init 把每一个元素初始化为一个集合,初始化后每一个元素的父亲节点是它本身。
- findRoot 查找一个元素所在的集合,其精髓是找到这个元素所在集合的祖先!
判断两个元素是否属于同一集合,只要看他们所在集合的祖先是否相同即可。
- union(x,y) 合并x,y所在的两个集合。合并两个不相交集合操作很简单:
利用 findRoot 找到其中两个集合的祖先,将一个集合的祖先指向另一个集合的祖先。

